import pandas as pd
import numpy as np
from scipy.linalg import toeplitz
def propensity_eq(x, cov_mat, R2_d=0.5):
dim_x = x.shape[1]
beta = [1 / (k**2) for k in range(1, dim_x + 1)]
b_sigma_b = np.dot(np.dot(cov_mat, beta), beta)
c_d = np.sqrt(np.pi**2 / 3. * R2_d/((1-R2_d) * b_sigma_b))
xx = np.exp(np.dot(x, np.multiply(beta, c_d)))
propensity_score = (xx/(1+xx))
return propensity_score
def potential_outcome_eq(x, cov_mat, R2_y=0.5, theta=0):
dim_x = x.shape[1]
beta = [1 / (k**2) for k in range(1, dim_x + 1)]
b_sigma_b = np.dot(np.dot(cov_mat, beta), beta)
c_y = np.sqrt(R2_y/((1-R2_y) * b_sigma_b))
d = 0
Y_0 = d * theta + d * np.dot(x, np.multiply(beta, c_y))
d = 1
Y_1 = d * theta + d * np.dot(x, np.multiply(beta, c_y))
return Y_0, Y_1
def make_irm_data(n_obs=500, dim_x=2, theta=0, R2_d=0.5, R2_y=0.5):
"""
Variation of DoubleML's make_irm_data function. Generates data for the interactive regression model (IRM) example and returns potential values
References
----------
Belloni, A., Chernozhukov, V., Fernández‐Val, I. and Hansen, C. (2017). Program Evaluation and Causal Inference With
High‐Dimensional Data. Econometrica, 85: 233-298.
"""
# inspired by https://onlinelibrary.wiley.com/doi/abs/10.3982/ECTA12723, see suplement
v = np.random.uniform(size=[n_obs, ])
zeta = np.random.standard_normal(size=[n_obs, ])
cov_mat = toeplitz([np.power(0.5, k) for k in range(dim_x)])
x = np.random.multivariate_normal(np.zeros(dim_x), cov_mat, size=[n_obs, ])
propensity_score = propensity_eq(x, cov_mat, R2_d)
D = 1. * (propensity_score > v)
Y_0, Y_1 = potential_outcome_eq(x, cov_mat, R2_y, theta)
Y = (1 - D) * Y_0 + D * Y_1 + zeta
x_flat = pd.DataFrame(x, columns=[f'x_{i}' for i in range(x.shape[1])])
df_orcl = pd.concat([pd.DataFrame({'Y_0': Y_0, 'Y_1': Y_1, 'ps': propensity_score, 'D': D, 'Y': Y}), x_flat], axis=1)
df = pd.concat([pd.DataFrame({'D': D, 'Y': Y}), x_flat], axis=1)
results = {'df': df, 'df_orcl': df_orcl}
return resultsSimulation Example: Propensity score trimming and reference population
Motivation example: Heterogeneous treatment effect and propensity score adjustments
Parameters \{a_1,a_2,b_1,b_2,c_1,c_2\} might be modified for tuning later.
np.random.seed(123)
R2_d= 0.35
R2_y= 0.35
dim_x = 2
theta = 0
n_obs = 1000
data_dict = make_irm_data(n_obs=n_obs, dim_x=dim_x, theta=theta, R2_d=R2_d, R2_y=R2_y)# Generate a histogram of propensity scores for treated and non-treated
import matplotlib.pyplot as plt
plt.hist(data_dict['df_orcl'].loc[data_dict['df_orcl']['D'] == 1, 'ps'], bins=20, alpha=0.5, label='Treated')
plt.hist(data_dict['df_orcl'].loc[data_dict['df_orcl']['D'] == 0, 'ps'], bins=20, alpha=0.5, label='Non-treated')
plt.xlabel('Propensity Score')
plt.ylabel('Frequency')
plt.title('Histogram of Propensity Scores')
min_ps_treated = data_dict['df_orcl'].loc[data_dict['df_orcl']['D'] == 1, 'ps'].min()
max_ps_treated = data_dict['df_orcl'].loc[data_dict['df_orcl']['D'] == 1, 'ps'].max()
min_ps_control = data_dict['df_orcl'].loc[data_dict['df_orcl']['D'] == 0, 'ps'].min()
max_ps_control = data_dict['df_orcl'].loc[data_dict['df_orcl']['D'] == 0, 'ps'].max()
# Compute the minimum and maximum propensity scores for treated and non-treated
print(min_ps_treated)
print(max_ps_treated)
# add vertical line at min_ps_treated and add label with value for min_ps_treated
plt.axvline(x=min_ps_treated, color='r', linestyle='--', label=f'Min PS Treated: {min_ps_control:.2f}')
plt.axvline(x=max_ps_control, color='r', linestyle='--', label=f'Max PS Control: {max_ps_control:.2f}')
# add legend below plot
plt.legend(loc='upper center', bbox_to_anchor=(0.5, -0.05), shadow=True, ncol=2)
plt.show()0.058309203265653316
0.9883990939718879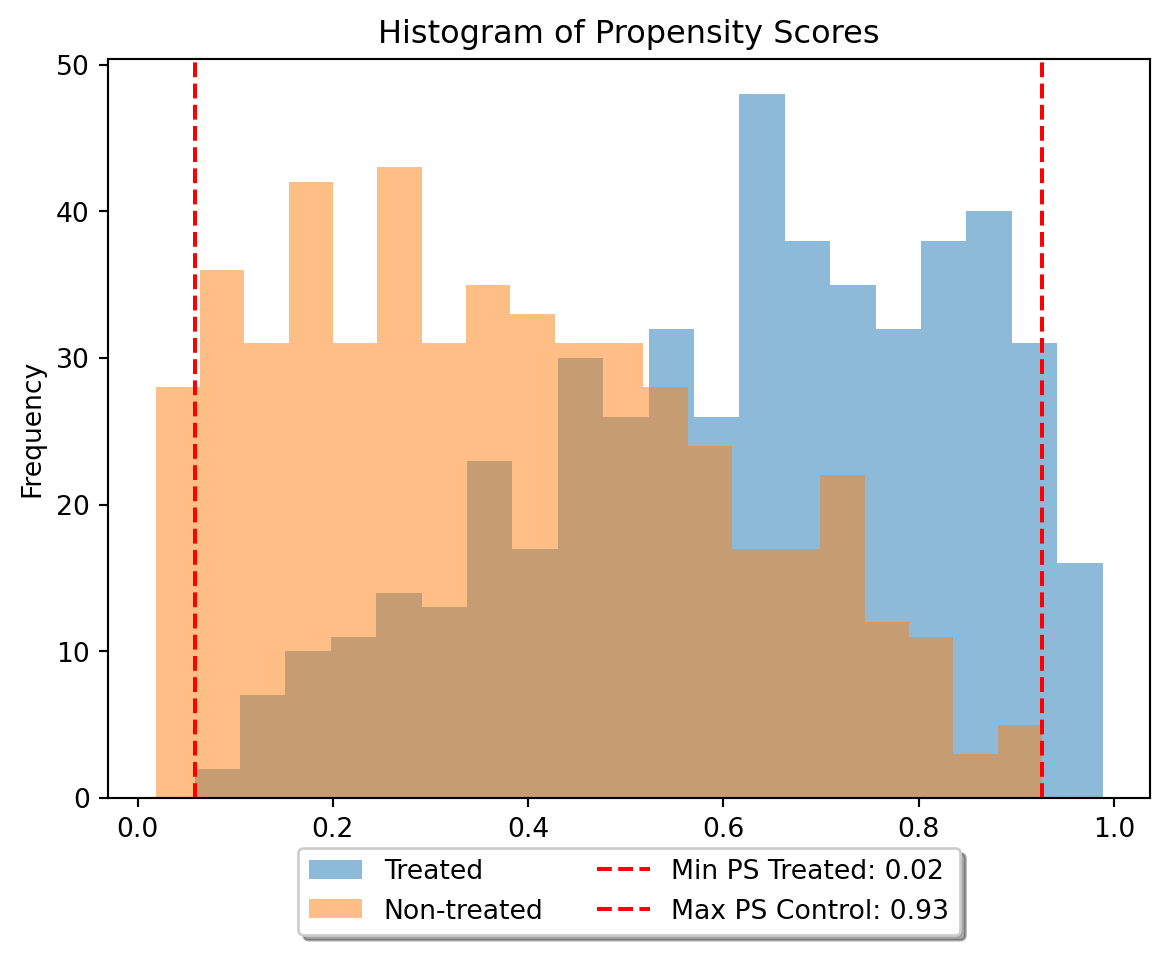
Summary of the propensity scores. This probably could be tuned more, but you can see that some areas have p_{treat} < 0.1 and thus trimming etc. might be advisable.
# summary of prop score
print(data_dict['df_orcl'].groupby('D')['ps'].describe()) count mean std min 25% 50% 75% \
D
0.0 511.0 0.375940 0.220918 0.018597 0.189679 0.355096 0.539133
1.0 489.0 0.624728 0.215901 0.058309 0.471686 0.648537 0.808571
max
D
0.0 0.926319
1.0 0.988399 Plot values of propensity score against values of X_1 and X_2 to illustrate what cutting off / clipping / discarding observations w.r.t. to the propensity score would imply in terms of the values of X_1 and X_2.
The surface plot shows that for high values of X_2, the propensity score varies a lot with X_1. Thus, we have “areas” of Overlap problems.
# create a plotly surface plot that maps the propensity value against all combinations of X_1 and X_2
import plotly.graph_objects as go
cov_mat = toeplitz([0.5**k for k in range(2)])
# Set up a grid for X_1 and X_2
x1 = np.linspace(-3, 3, 100)
x2 = np.linspace(-3, 3, 100)
X_1, X_2 = np.meshgrid(x1, x2)
# prepare array for propensity scores (100x100)
propensity_score = np.zeros((x1.shape[0], x2.shape[0]))
# for each combination of X_1 and X_2, compute the propensity score
for i in range(x1.shape[0]):
for j in range(x2.shape[0]):
x = np.array([X_1[i,j], X_2[i,j]]).reshape(1,2)
cov_mat = toeplitz([np.power(0.5, k) for k in range(dim_x)])
ps_score = propensity_eq(x, cov_mat, R2_d)
propensity_score[i,j] = ps_score/tmp/ipykernel_29464/3782873549.py:19: DeprecationWarning:
Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
fig = go.Figure(data=[go.Surface(z=propensity_score, x=X_1, y=X_2)])
fig.update_layout(title='Propensity score surface plot', autosize=False, width=500, height=500)
# Show plot
fig.show()# Create a df with propensity score and values for X_1 and X_2
propensity_df = pd.DataFrame({'X_1': X_1.flatten(), 'X_2': X_2.flatten(), 'ps': propensity_score.flatten()})We implement trimming for propensity scores smaller than 0.1
# indicator for being trimmed from above, i.e., if ps > 1-trim_val
trim_val = 0.1
propensity_df['trim_top'] = np.where(propensity_df['ps'] > 1-trim_val, 1, 0)
propensity_df['trim_bottom'] = np.where(propensity_df['ps'] < trim_val, 1, 0)18.75\% of the observations get trimmed from above (because their p_{treat} > 0.9 ) and 18.75\% (because p_{treat} <0.1).
# share of trimmed
propensity_df[["trim_top", "trim_bottom"]].mean()*100trim_top 18.75
trim_bottom 18.75
dtype: float64# create a heatmap uisng propensity_df
import plotly.express as px
fig = px.density_heatmap(propensity_df, x='X_1', y='X_2', z='ps', title='Propensity score heatmap', histfunc = 'avg', nbinsx=100, nbinsy=100)
# Compute values of X_1 and X_2 for which the propensity score is greater than trim_val
trim_val = 0.1
propensity_df['trimmed'] = (propensity_df['ps'] < trim_val).astype(int) | (propensity_df['ps'] > 1-trim_val).astype(int)
share_trimmed = propensity_df['trimmed'].mean()
# Add title to the plot
fig.update_layout(title=f'Propensity score heatmap with trim_val = {trim_val}, Share of trimmed obs: {share_trimmed*100}%')
fig.show()The next plot shows the propensity score only for the untrimmed subpopulation. Note: On the top left observations are missing, that we “trimmed”
# Heat map for only untrimmed observations
# filter out trimmed observations
propensity_df_untrimmed = propensity_df[propensity_df['trimmed'] == 0]
fig = px.density_heatmap(propensity_df_untrimmed, x='X_1', y='X_2', z='ps', title='Propensity score heatmap for untrimmed observations', histfunc = 'avg', nbinsx=100, nbinsy=100)
# Add title to the plot
fig.update_layout(title=f'Propensity score heatmap for untrimmed observations')Next, we want to look at the potential outcomes for the different areas of X_1, X_2. We see, that the average Y_0 and Y_1 is very high in the trimmed area - does this lead to problems maybe? Is the population still the same even though we trimmed?
# Add potential outcomes to propensity_df
Y_0, Y_1 = potential_outcome_eq(x = propensity_df.loc[:, ['X_1', 'X_2']], cov_mat=cov_mat, R2_y=R2_y, theta=theta)
propensity_df['Y_0'] = Y_0
propensity_df['Y_1'] = Y_1# Heatmap for Y_0 based on untrimmed obs only
propensity_df_untrimmed = propensity_df[propensity_df['trimmed'] == 0]
fig = px.density_heatmap(propensity_df_untrimmed, x='X_1', y='X_2', z='Y_0', title='Potential outcome Y_0 heatmap for untrimmed observations', histfunc = 'avg', nbinsx=100, nbinsy=100)
# Add title to the plot
fig.update_layout(title=f'Potential outcome Y_0 heatmap for untrimmed observations')
fig.show()# Heatmap for Y_1 based on untrimmed obs only
fig = px.density_heatmap(propensity_df_untrimmed, x='X_1', y='X_2', z='Y_1', title='Potential outcome Y_1 heatmap for untrimmed observations', histfunc = 'avg', nbinsx=100, nbinsy=100)
# Add title to the plot
fig.update_layout(title=f'Potential outcome Y_1 heatmap for untrimmed observations')
# Heatmap for Y based on untrimmed obs only
fig.show()Compare untrimmed to trimmed data in terms of distribution of X_1 and X_2. You can tell, that we bite out a corner of the distribution :)
# Plot joint density of X_1 and X_2
# Creating a 2D histogram
fig = px.density_heatmap(propensity_df, x='X_1', y='X_2', nbinsx=30, nbinsy=30, color_continuous_scale='Blues')
# Updating layout for better readability
fig.update_layout(
title='2D Histogram using Plotly',
xaxis_title='X-axis',
yaxis_title='Y-axis',
coloraxis_colorbar=dict(title='Counts')
)
# Show the plot
fig.show()# Plot joint density of X_1 and X_2
# Creating a 2D histogram
fig = px.density_heatmap(propensity_df_untrimmed, x='X_1', y='X_2', nbinsx=30, nbinsy=30, color_continuous_scale='Blues')
# Updating layout for better readability
fig.update_layout(
title='2D Histogram using Plotly',
xaxis_title='X-axis',
yaxis_title='Y-axis',
coloraxis_colorbar=dict(title='Counts')
)
# Show the plot
fig.show()Next steps/ open questions
- What could be done next is to simulate data, estimate with DoubleML and then assess how the trimming affects the distribution of X_1 and X_2 as compared to the reference population. Do different trimming rules (truncation, discarding) lead to different results?
- So far, we considered a simple linear model with a constant effect of D on Y. If the effect (i.e. Y_1 - Y_0 is allowed to vary with X_1 and X_2, trimming/discarding might lead to non-random sample selection
- The example was based on uniformly distributed covariates… it might make sense to look at other distributions, e.g. joint normal
Example:
from doubleml import DoubleMLIRM, DoubleMLData
from lightgbm import LGBMClassifier, LGBMRegressor
from sklearn.model_selection import cross_val_predict- “Truncation”
np.random.seed(1234)
results = []
num_repetitions = 1
for i in range(num_repetitions):
result_i = []
true_theta = 1
df_dict = make_irm_data(n_obs=n_obs, dim_x=dim_x, theta=theta, R2_d=R2_d, R2_y=R2_y)
data = DoubleMLData(df_dict['df'], 'Y', 'D', ['x_0', 'x_1'])
ml_g, ml_m = LGBMRegressor(verbose = -1), LGBMClassifier(verbose = -1)
for trimming_value in [0.001, 0.01, 0.05, 0.1]:
dml_obj = DoubleMLIRM(data, ml_g, ml_m, trimming_threshold=trimming_value)
dml_obj.fit()
result_i.append(dml_obj.coef[0] - true_theta) # append bias of trimming value
results.append(result_i) # append result of repetition i/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for D is not positive. Re-estimation based on riesz representer (non-orthogonal).
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for D is not positive. Re-estimation based on riesz representer (non-orthogonal).
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for D is not positive. Re-estimation based on riesz representer (non-orthogonal).
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
result_frame = pd.DataFrame(results, columns=["trim 0.001", "trim 0.01", "trim 0.05", "trim 0.1"])
result_frame| trim 0.001 | trim 0.01 | trim 0.05 | trim 0.1 | |
|---|---|---|---|---|
| 0 | -0.528917 | -0.744113 | -0.915383 | -0.921815 |
- “Discarding”
np.random.seed(1234)
results = []
num_repetitions = 1
for i in range(num_repetitions):
result_i = []
# make data
df_dict = make_irm_data(n_obs=n_obs, dim_x=dim_x, theta=theta, R2_d=R2_d, R2_y=R2_y)
data = df_dict['df']
# make estimators
ml_g, ml_m = LGBMRegressor(verbose = -1), LGBMClassifier(verbose = -1)
# estimate pscore
data["pscore_est"] = cross_val_predict(ml_m, data.drop(columns=["Y", "D"]), data.D, method='predict_proba')[:,1]
for trimming_value in [0.001, 0.01, 0.05, 0.1]:
# discard poor overlap
data_trimmed = data.loc[~((data["pscore_est"] < trimming_value) | (data["pscore_est"] > 1 - trimming_value))].drop(columns=["pscore_est"])
# create dml data obj
dml_data = DoubleMLData.from_arrays(x=data_trimmed.drop(columns=["Y", "D"]),
y=data_trimmed["Y"],
d=data_trimmed["D"])
dml_obj = DoubleMLIRM(dml_data, ml_g, ml_m, trimming_threshold=1e-12) # set trimming very low because we already discarded
dml_obj.fit()
result_i.append(dml_obj.coef[0] - true_theta) # append bias of trimming value
results.append(result_i) # append result of repetition i/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for d is not positive. Re-estimation based on riesz representer (non-orthogonal).
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for d is not positive. Re-estimation based on riesz representer (non-orthogonal).
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for d is not positive. Re-estimation based on riesz representer (non-orthogonal).
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/deprecation.py:151: FutureWarning:
'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/opt/hostedtoolcache/Python/3.9.24/x64/lib/python3.9/site-packages/doubleml/double_ml.py:1479: UserWarning:
The estimated nu2 for d is not positive. Re-estimation based on riesz representer (non-orthogonal).
dml_obj.predictions["ml_m"].flatten()>0.1array([ True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, False, True, True, True, True, True,
False, True, True, True, True, False, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, False,
True, True, True, True, True, True, True, True, True,
True, True, True, False, True, True, True, True, True,
True, True, True, False, True, True, True, True, True,
True, True, True, True, True, True, True, True, False,
True, True, True, True, False, True, True, True, True,
False, False, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, False, True, True, True, True, True,
False, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, False, True, False, True, False, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, False, True, True, True, True, True,
False, False, False, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, False, True, True, False, True, True, True, True,
False, True, True, True, True, True, True, True, False,
False, True, True, True, True, False, False, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, False, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, False, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, False, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, False, True, True, True, True,
True, True, True, True, True, True, False, True, True,
True, False, True, True, True, False, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, False, False, True, True, True, True, True, True,
True, True, False, True, True, True, True, True, True,
True, True, True, True, False, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, False, True, True, True, False, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, False, False, True, False, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, False, False, True, True,
True, True, True, True, False, True, True, True, True,
True, True, True, True, True, True, True, True, True,
False, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, False, True, True, True, True, True,
False, False, True, True, True, True, False, False, True,
True, True, True, True, True, False, False, True, True,
True, True, True, True, True, False, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, False, True, True, True, True, True, False,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, False, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, False, False,
True, True, True])result_frame = pd.DataFrame(results, columns=["trim 0.001", "trim 0.01", "trim 0.05", "trim 0.1"])
result_frame| trim 0.001 | trim 0.01 | trim 0.05 | trim 0.1 | |
|---|---|---|---|---|
| 0 | -0.528917 | -1.484421 | -1.070437 | -0.504971 |
TODO: Look at trimmed and untrimmed distributions, look at distributions of potential outcomes, look at bias.